Affine and convex sets

仿射集合和凸集

1. Lines and line segments

$y=\theta x_1+(1-\theta)x_2$，$x_1 \ne x_2$。

  • if $\theta \in R$，y就是个line

  • if $0\le \theta \le1$，y就是line segments

2. Affine set （仿射集）

A set $C \in R^n$ is affine if the line through any two distinct points in $C$ lies in $C$, i.e. if for any $x_1, x_2 ∈ C$ and $\theta \in R$, we have $\theta x_1+(1-\theta)x_2 \in C$.

对于集合C中的任意两个不相同的点$x_1,\ x_2$, 点$\theta x_1+(1-\theta)x_2$也在集合C中，且对于$\theta \in R$都成立，则C就叫仿射集。

Affine combination (仿射组合)：$\theta_1x_1+…+\theta_kx_k$ (where $\theta_1+…+\theta_k=1$) 就是点$x_1,..,x_k$的仿射组合

Subspace (子空间)： $V=C-x_0={x-x_0 x \in C }$ (C is a affine set)
Affine hull (仿射包) aff $C={\theta_1x_1+…+\theta_kx_k x_1,..,x_k \in C,\theta_1+…+\theta_k=1}$
  • The affine hull is the smallest affine set tha contains $C$
  • Affine dimension (仿射维度)： the affine dimension of a set $C$ is the dimension of its affine hull.
  • relative interior (相对内部)： if the affine dimension of a set $C \subseteq R^n$ is less than $n$, then the affine set aff $C \ne R^n$. so the relative interior of the set $C$ is **relint **$C={x \in C B(x,r) \cap \rm{aff} C \subseteq C\rm{\ for\ some\ }r >0 }$, where $B(x,r)={y \left|y-x \right| \le r}$.
  • relative boubdary (相对边界)： cl $C$ is the closure of $C$

3. Convex sets (凸集)

A set $C$ is convex if the line segment between any two points in $C$ lies in $C$, i.e. if for any $x_1, x_2 ∈ C$ and any $0\le\theta \le1$, we have $\theta x_1+(1-\theta)x_2 \in C$.

对于集合C中的任意两个不相同的点$x_1,\ x_2$, 点$\theta x_1+(1-\theta)x_2$也在集合C中，且对于$0\le\theta \le1$都成立，则C就叫凸集。

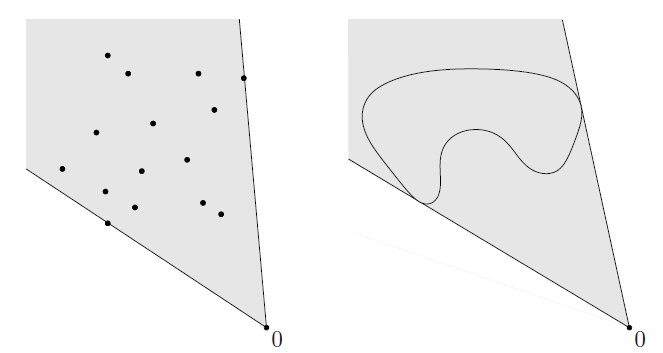
Convex combination (凸组合)：$\theta_1x_1+…+\theta_kx_k$ (where $\theta_1+…+\theta_k=1$， $\theta_i \ge 0,i=1,…,k$) 就是点$x_1,..,x_k$的凸组合

Convex hull (凸包): conv $C={\theta_1x_1+…+\theta_kx_k x_1,..,x_k \in C,\theta_1+…+\theta_k=1,\theta_i\ge0,i=1,…,k}$

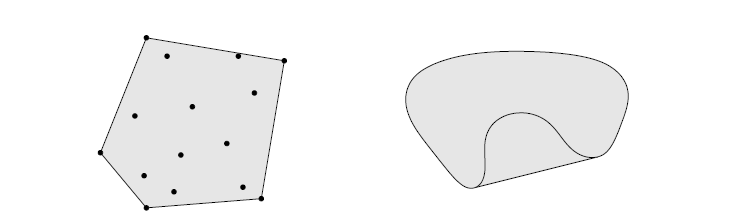
Left. 阴影部分就是那15个点形成的凸包

Right. 阴影部分是Kidney shaped set的凸包

Cones (锥)

Convex cone (凸锥): $\theta_1x_1+\theta_2x_2 \in C$ ,for any $x_1,x_2 \in C$ and $\theta_1,\theta_2\ge0$

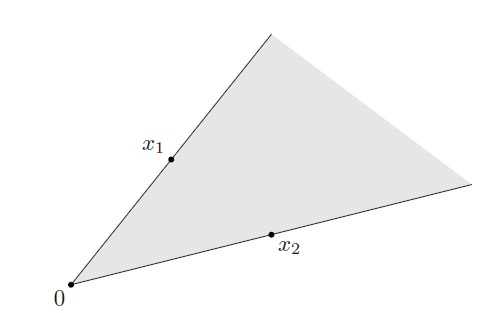
Conic combination (锥组合)：$\theta_1x_1+…+\theta_kx_k$ (where $\theta_1+…+\theta_k\ge1$) 就是点$x_1,..,x_k$的锥组合(or nonnegation linear combination)

Conic hull (锥包)：${\theta_1x_1+…+\theta_kx_k x_1,..,x_k \in C,\theta_i\ge0,i=1,…,k}$

下图就是两个集合的锥包

Some important examples

1. Hyperplane and halfspace

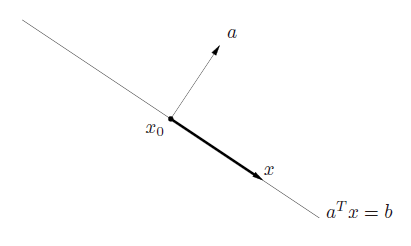
**Hyperplane (超平面): **${x a^Tx=b}$, where $a\in R^n,a\ne0,b\in R$
  • $a$: normal vector (法线)
  • $b$ determines the offset of the hyperplane from the origin
  • hyperplanes are affine and convex
  • ${x a^T(x-x_0)=0}$

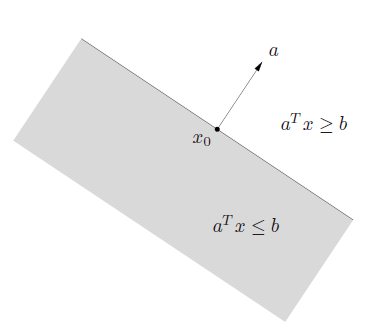
Halfspace (半平面)：${x a^Tx \le b}$, where $a\ne0$
  • halfspaces are convex, but not affine.
  • $a$ is the outward normal vector.
  • open halfspace: ${x a^Tx < b}$

2. Euclidean ball and ellipsoid（Euclidean 球和椭球）

**Euclidean ball: **$B(x_c,r)={x \left| x-x_c \right|_2 \le r}={x (x-x_c)^T (x-x_c)\le r^2}={x_c+ru \left| u\right |_2 \le 1}$
  • $\left | \cdot \right|$ denotes the Euclidean norm
Ellipsoid: $\cal E={x (x-x_c)^TP^{-1}(x-x_c)\le1}$ where$P=P^T\succ0$
  • $P$ is symmtric and positive definite (对称，正定)。
  • a ball is an ellipsoid with $P=r^2I$
  • $\cal E={x_c+Au \left | u\right |_2 \le 1}$ where A is square and nonsingular (非奇异的方阵)

3. Norm balls and norm cones

**Norm ball (范数球): ** ${x \left|x-x_c \right |\le r}$
**Norm cone (范数锥): ** $C={(x,t) \left|x \right |\le t} \sube R^{n+1}$
  • norm balls and cones are convex

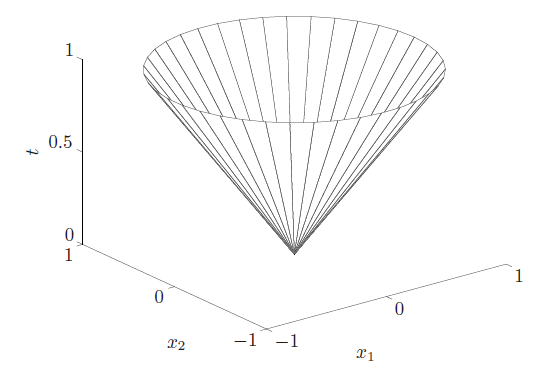
4. Polyhedra

Polyhedron (多面体): ${\cal P}={a_j^Tx \le b_j,j=1,…,m,c_j^Tx=d_j,j=1,…,p}$

Polyhedra是Polyhedron的复数

  • $Ax \preceq b$, $Cx=d$, where $A \in R^{m \times n}, C \in R^{p \times n}$

  • $\preceq$ is componentwise inequality (分量不等式)

    也就是前面矩阵按照每个元素小于等于后面矩阵的对应元素。

  • * Simplexes 单纯形

  • * Convex hull description of polyhedra

Polytope (多胞形)：A bounded polyhedron is sometimes called a polytope.

Polyhedron和polytope有的教材会翻过来定义。不用太追究就好。

5. The positive semidefinite cone （半正定锥）

  • $S^n$ denotes symmetric $n \times n$ matrix, $S^n={X\in R^{n\times n} X=X^T}$, which is a vector space with dimension $n(n+1)/2$

    这里向量空间维度为什么是$n(n+1)/2$呢？

    比如矩阵$X = \left[ {\begin{array}{*{20}{c}}x&y\y&z\end{array}} \right]\in S^n$。因为要保持对称，所以副对角线的元素都是$y$, 因此对于$n=2$的向量空间维度为3。

    再如果$X\in S_+^n$是一个半正定对称矩阵的话。

    则满足$x\ge 0,z\ge0,xz\ge y^2$。所以可得到一个Positive semidefinite cone.

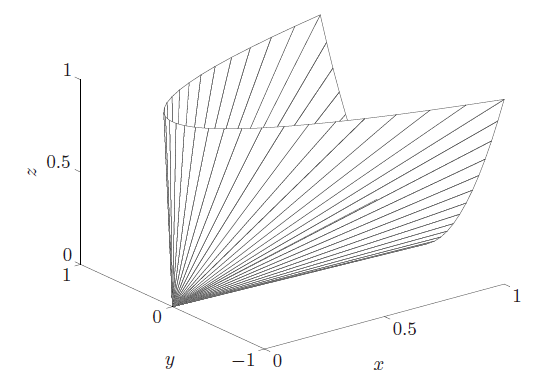
  • $S_+^n$ denotes the set of symmetric positive semidefinite matrix, $S_+^n={X\in S^n X\succeq0 }$
  • $S_{++}^n$ denotes the set of symmetric positive definite matrix, $S_+^n={X\in S^n X\succ 0 }$

Remark1: Positive definite matrices and Positive semidefinite matrices

参考有人总结的文章浅谈「正定矩阵」和「半正定矩阵」

【定义1】给定一个大小为$n \times n$ 的实对称矩阵$A$，若对于任意长度为$n$的非零向量$x$，有$x^TAx>0$恒成立，则矩阵 $A$是一个正定矩阵。

【定义1】给定一个大小为$n \times n$ 的实对称矩阵$A$，若对于任意长度为$n$的非零向量$x$，有$x^TAx \ge0$恒成立，则矩阵 $A$是一个半正定矩阵。

正定矩阵和半正定矩阵的直观解释

若给定任意一个正定矩阵$A\in \cal R^{n \times n}$和一个非零向量 $x\in \cal R^{n}$ ，则两者相乘得到的向量$y=Ax\in \cal R^n$与向量$x$角恒小于$\frac{\pi}{2}$ . (等价于: $x^TAx>0$)

若给定任意一个正定矩阵$A\in \cal R^{n \times n}$和一个非零向量 $x\in \cal R^{n}$ ，则两者相乘得到的向量$y=Ax\in \cal R^n$与向量$x$角恒小于或等于$\frac{\pi}{2}$ . (等价于: $x^TAx\ge0$)

根据上面的理解，在结合之前在Essence of Linear Algebra系列笔记整理的学习中对线性代数的理解。

将向量$x$作变换矩阵为$A$的线性变换，得到向量新的向量$Ax$, 则$\vec {Ax}$与原来$\vec x$的夹角则决定了变换矩阵$A$是正定的还是半正定的。

正定矩阵的性质

  • 正定矩阵的行列式恒为正；

  • 实对称矩阵$A$正定当且仅当$A$与单位矩阵合同；

    合同变换（congruent transformation）是指在平面到自身的一一变换下，任意线段的长和它的像的长总相等，这种变换也叫做全等变换，或称合同变换。

  • 两个正定矩阵的和是正定矩阵；

  • 正实数与正定矩阵的乘积是正定矩阵。

正定矩阵的等价命题

  1. $A$是正定矩阵；
  2. $A$的一切顺序主子式均为正；
  3. $A$的一切主子式均为正；
  4. $A$的特征值均为正；
  5. 存在实可逆矩阵$C$，使$A=C’C$；
  6. 存在秩为$n$的$m\times n$实矩阵$B$，使$A=B’B$；
  7. 存在主对角线元素全为正的实三角矩阵$R$，使$A=R’R$

Remark 2: Various norms

此部分主要参考了0范数，1范数，2范数的区别

向量范数

1-范数：$\left | x\right |1=\sum\limits{i = 1}^N {\left \right }$

2-范数：$\left | x\right |2=\sqrt{\sum\limits{i = 1}^N {x_i^2} }$ ，也叫Euclidean norm/distance

$\infty$-范数： $\left | x\right |_\infty=\mathop }\limits_i {\left \right }$
$-\infty$-范数： $\left | x\right |_{-\infty}=\mathop }\limits_i {\left \right }$
p-范数：$\left | x\right |p=\left(\sum\limits{i = 1}^N {\left x_i \right ^p}\right)^{\frac{1}{p}} $

矩阵范数

1-范数：$\left | A\right |1=\mathop }\limits_j \sum\limits{i = 1}^m {\left } \right }$, 列和范数

2-范数：$\left | A\right |_2=\sqrt{\lambda_1}$ ，$\lambda_1$ 为$A^TA$的最大特征值，谱范数

$\infty$-范数：$\left | A\right |\infty=\mathop }\limits_i \sum\limits{j = 1}^n {\left } \right }$ , 行和范数
F-范数：$\left | A\right |F=\left(\sum\limits{i = 1}^m \sum\limits_{j = 1}^n {\left a_{i,j}\right ^2}\right)^{\frac{1}{p}} $, Frobenius范数

核范数：$\left | A\right |*= \sum\limits{i = 1}^n { \lambda_i }$, $\lambda_i$是矩阵$A$的奇异值

一下是不同的norm对应的曲线。

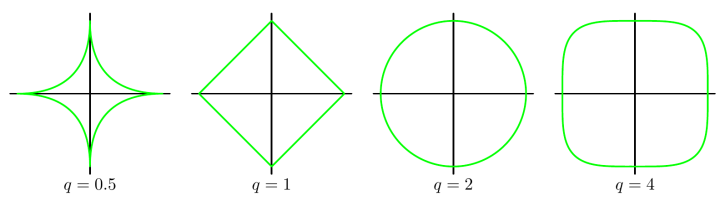
上图中，可以明显看到一个趋势，即$q$越小，曲线越贴近坐标轴，$q$越大，曲线越远离坐标轴，并且棱角越明显。那么 $q=0 $和 $q=\infty$ 时极限情况如何呢？猜猜看。

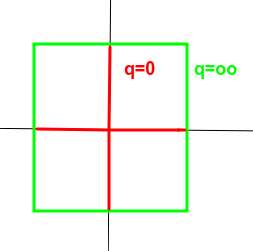
答案就是十字架和正方形。除了图形上的直观形象，在数学公式的推导中，$q=0 $和 $q=\infty$时两种极限的行为可以简记为非零元的个数和最大项。即0范数对应向量或矩阵中非零元的个数，无穷范数对应向量或矩阵中最大的元素。

Remark3: Singular matrix and Nonsingular matrix

Singular matrix (奇异矩阵): 行列式为0的矩阵

Nonsingular matrix (非奇异矩阵): 行列式不为0 的矩阵

  • 一个矩阵非奇异当且仅当它的行列式不为零。
  • 一个矩阵非奇异当且仅当它代表的线性变换是个自同构。
  • 一个矩阵半正定当且仅当它的每个特征值大于或等于零。
  • 一个矩阵正定当且仅当它的每个特征值都大于零。
  • 一个矩阵非奇异当且仅当它的秩为n

Remark4 :Singular Value Decomposition（SVD）

奇异值分解这部分主要参考了奇异值分解（SVD）

1. 回顾特征值和特征向量

$Ax=\lambda x$

where $A\in R^{n\times n}, x\in R^n$. hence, $\lambda$ is its eigenvalue, $x$ is the eigenvector of $\lambda$.

求出特征值和特征向量有什么好处呢？ 就是我们可以将矩阵A特征分解。如果我们求出了矩阵$A$的$n$个特征值$\lambda_1 \le \lambda_2 \le …\le\lambda_n$，以及这$n$个特征值所对应的特征向量$w_1,w_2,…,w_n$.

那么矩阵A就可以用下式的特征分解表示：

$A=W\Sigma W^{-1}$

其中$W$是这$n$个特征向量所张成的$n \times n$维矩阵, 而$\Sigma $为这$n$个特征值为主对角线的$n \times n$维矩阵。

一般我们会把W的这n个特征向量标准化，即满足$\left | w_i\right |_2=1$ ，或者$ w_i^T w_i=1$ ，此时W的

$n$个特征向量为标准正交基，满足$W^TW=I$, 即$W^T=W^{-1}$，也就是说$W$为酉矩阵。

这样我们的特征分解表达式可以写成

$A=W \Sigma W^{T}$

注意到要进行特征分解，矩阵A必须为方阵。

那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了。

2. SVD的定义

SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵$A$是一个$m \times n$的矩阵，那么我们定义矩阵$A$的SVD为：

$A=U \Sigma V^T$

其中$U$是一个$m \times m$的矩阵, $\Sigma$ 是一个$m \times n$的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值, $V$是一个$n \times n$ 的矩阵。$U$ 和$V$都是酉矩阵，即满足$U^TU=I, V^TV=I$ 。下图可以很形象的看出上面SVD的定义：

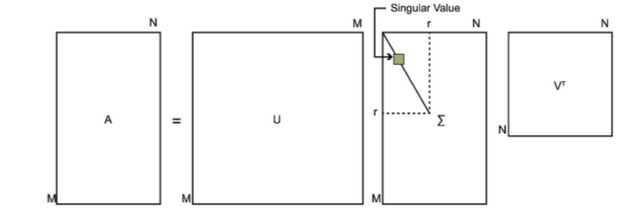
那么我们如何求出SVD分解后的$U,\Sigma,V$这三个矩阵呢？

如果我们将$A$的转置和$A$做矩阵乘法，那么会得到$n\times n$的一个方阵$A^TA$。既然$A^TA$是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

$(A^TA)v_i=\lambda_iv_i$

这样我们就可以得到矩阵 $A^TA$ 的$n$个特征值和对应的$n$个特征向量$v$了。将 $A^TA$ 的所有特征向量张成一个$n \times n$的矩阵$V$，就是我们SVD公式里面的$V$矩阵了。一般我们将$V$中的每个特征向量叫做$A$的右奇异向量。

如果我们将A和A的转置做矩阵乘法，那么会得到$m\times m$的一个方阵 $AA^T$ 。既然 $AA^T$ 是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

$(AA^T)u_i=\lambda_iu_i$

这样我们就可以得到矩阵 $AA^T$ 的$m$个特征值和对应的$m$个特征向量$u$了。将 $AA^T$ 的所有特征向量张成一个$m \times m$的矩阵$U$，就是我们SVD公式里面的$U$矩阵了。一般我们将$U$中的每个特征向量叫做$A$的左奇异向量。

$U$和$V$我们都求出来了，现在就剩下奇异值矩阵$\Sigma$没有求出了.由于$\Sigma$除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值$\sigma$就可以了。我们注意到:

$A=U \Sigma V^T \Rightarrow AV=U \Sigma V^TV \Rightarrow AV=U\Sigma \Rightarrow Av_i=\sigma_iu_i \Rightarrow \sigma_i=\frac{Av_i}{u_i}$

这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵$\Sigma$。

$A=U \Sigma V^T \Rightarrow A^T=V \Sigma U^T \Rightarrow A^TA=V\Sigma U^TU \Sigma V^T=V\Sigma^2V^T$

以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：

$\sigma_i=\sqrt{\lambda_i}$

3. SVD的一些性质

对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。

也就是说，我们也可以用最大的$k$个的奇异值和对应的左右奇异向量来近似描述矩阵。

也就是说：

$A_{m\times n}=U_{m\times m}\Sigma_{m\times n}V_{n\times n}^T \approx U_{m\times k}\Sigma_{k\times k}V_{k\times n}^T$

其中$k$要比$n$小很多，也就是一个大的矩阵A可以用三个小的矩阵$U_{m\times k},\Sigma_{k\times k},V_{k\times n}^T$来表示。如下图所示，现在我们的矩阵$A$只需要灰色的部分的三个小矩阵就可以近似描述了。

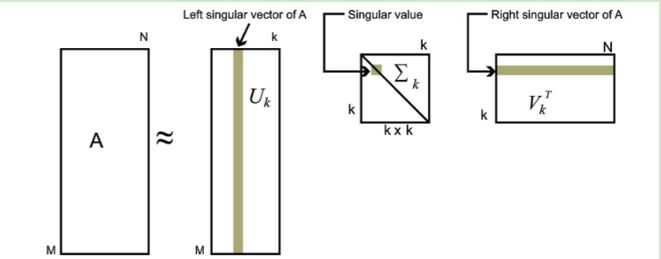
由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。

下面我们就对SVD用于PCA降维做一个介绍。

4. SVD用于PCA

PCA降维，需要找到样本协方差矩阵$X^TX$的最大的$d$个特征向量，然后用这最大的$d$个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵$X^TX$，当样本数多样本特征数也多的时候，这个计算量是很大的。

注意到我们的SVD也可以得到协方差矩阵$X^TX$最大的$d$个特征向量张成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵$X^TX$，也能求出我们的右奇异矩阵$V$。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。

另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？

假设我们的样本是$m \times n$的矩阵$X$，如果我们通过SVD找到了矩阵$XX^T$最大的$d$个特征向量张成的$m\times d$维矩阵$U$，则我们如果进行如下处理：

$X_{d \times n}^\prime =U_{d\times m}^TX_{m \times n}$

可以得到一个$d\times n$的矩阵$X^\prime$,这个矩阵和我们原来的$m\times n$维样本矩阵$X$相比，行数从$m$减到了$d$，可见对行数进行了压缩。

左奇异矩阵可以用于行数的压缩。

右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。

SVD作为一个很基本的算法，在很多机器学习算法中都有它的身影，特别是在现在的大数据时代，由于SVD可以实现并行化，因此更是大展身手。

SVD的缺点是分解出的矩阵解释性往往不强，有点黑盒子的味道，不过这不影响它的使用。

Operations that preserve convexity (保凸运算)

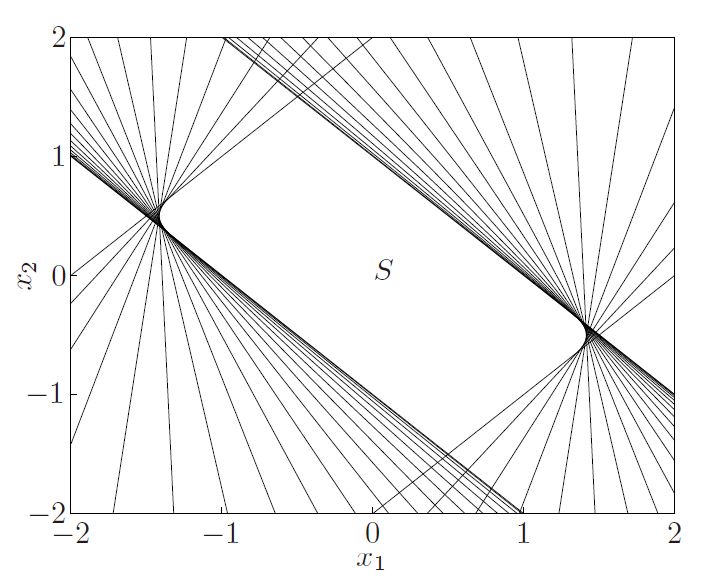
1. Intersection (交集)

the intersection of (any nomber of) convex sets is convex

example:

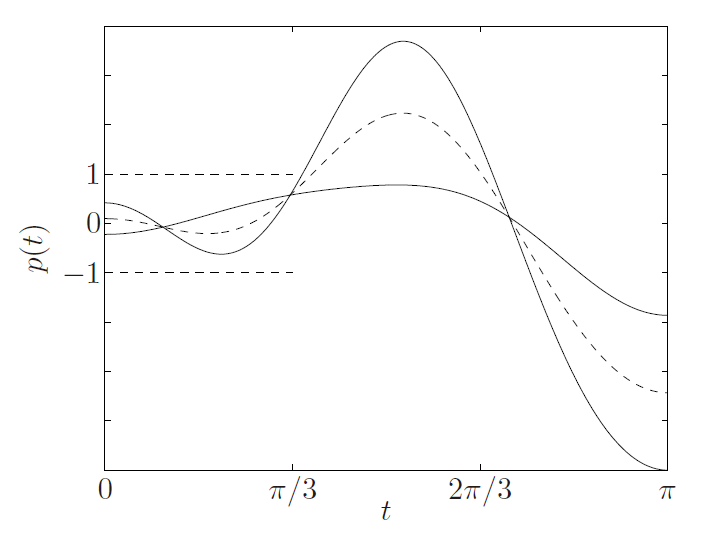
$S={ x\in R^m \left p(t)\right \le1 for t \le\pi/3 }=\cap_{ t \le\pi/3}{ x   p(t) \le 1}$

其中$p(t)=x_1cost+x_2cos2t+\cdot\cdot\cdot +x_mcosmx$

  1. 证明S(t)是凸的

图中两个实线是随机选取的在$ t \le\pi/3$时满足$ p(t) \le 1$的曲线。相当于在集合中选取的两个点$(x,y)$，然后看$\theta x+(1-\theta)y$是否也满足$ p(t) \le 1$，即也在集集合中。图中的虚线就是取的$\theta=1/2$时的情况，可以看到在$ t \le\pi/3$仍然满足$ p(t) \le 1$，即$\theta x+(1-\theta)y$也在集集合中。得证$S$是凸集
  1. 下图绘制出了当$m=2$时的集合图
$S={ x\in R^m \left x_1cost+x_2cos2t \right \le1 for t \le\pi/3 }$
其中$x_1cost+x_2cos2t$是一个line，$\left x_1cost+x_2cos2t \right \le1$就是两个line和中间的部分组成的slab(平板)。当$t$取值不同时，曲线的斜率也不同。就构成了无数个slabs。将这些slabs取交集便是$S$

2. Affine function

$f:R^n \to R^m$

$f(x)=Ax+b$, where $A \in R^{m \times n}, b\in R^m$

image: $f(S)={ f(x) x \in S}$
**inverse image: ** $f^{-1}(S)={ x f(x) \in S}$

Both image and inverse image can peserve convexity

这里f(x)也可以说是linear，但是linear是informal说法，affine比较正式

Examples

  • scalling: $\alpha S={\alpha x x\in S}$
  • **translation: **$S+a={x+a x\in S}$
  • **projection: ** $T={ x\in R^m (x_1,x_2)\in S\sube R^m\times R^n \rm{for\ some\ } x_2\in R^n}$
  • **sum: **$S_1+S_2={x+y x\in S_1,y\in S_2}$
  • **Cartesian product: **$S_1\times S_2={(x_1,x_2) x_1\in S_1,x_2\in S_2}$
  • **partial sum: ** $S={(x,y_1+y_2) (x,y_1)\in S_1,(x,y_2)\in S_2}$
  • **polyhedron: **${x Ax \preceq b,Cx=d }={ x f(x)\in R_+^m\times{ 0} }$, $f(x)=(b-Ax,d-Cx)$
  • **solution of linear matrix inequlity: ** ${x A(x) \preceq B}={ x f(x)\in R_+^m}$, $f(x)=B-A(x),f:R^n \to R^m$
  • Hyperbolic cone (双曲线锥)：${x x^TPx\le(c^Tx)^2, c^T x \ge 0 }=f^{-1}({ (z,t) z^Tz\le t^2,t \ge 0 })$, where $P\in S_+^n,c\in R^n,f(x)=(P^{1/2}x,c^Tx)$.

3. Linear-fractional and perspective function

perspective function: **$P:R^{n+1} \to R^n$ with domain **dom $P=R^n \times R_{++}$, $P(z,t)=z/t$

  • perspective function(透视函数) 也是保凸的

  • the inversr image is also convex $P^{-1}(C)={(x,t)\in R^{n+1} x/t\in C,t>0}$

  • 可将之形象的理解成小孔成像，将3D图像映射到2D底板上。

    $x_3$相当于第$n+1$列的数值都变成了全部相同的数字，因此直接舍去。

Linear-fractional function

$g:R^n \to R^{m+1}$, $g(x)=\left[ \begin{array}{l}{\rm{A}}\{c^T}\end{array} \right]x + \left[ \begin{array}{l}b\d\end{array} \right]$. where $A\in R^{m \times n},b\in R^m,c \in R^n$

$f:R^n \to R^m, $$f=P \circ g$, $f(x)=\frac{Ax+b}{c^Tx+d}, \mathbf{dom}f={ x c^Tx+d >0}$

Generalized inequalities

1. proper cone（正常锥）

  • $K$ is convex
  • $K$ is closed
  • $K$ is solid, which means it has nonempty interior.(实心的)
  • $K$ is pointed, which means that it contains no line（尖的）

so, $K \sube R^n$ is called a proper cone

2. partical ordering（偏序）

  • partical ordering：$x \preceq_K y \Leftrightarrow y-x \in K$
  • strict partical ordering：$x \prec_K y \Leftrightarrow y-x \in {\mathbf{int}}K$
  • componentwise inequality
  • matrix inequality:
    • $S_+^n$ is a proper cone in $S^n$ : positive semidefinite cone
    • $X \preceq_K Y \Leftrightarrow Y-X$ is a positive semidefinite
    • $X \prec_K Y \Leftrightarrow Y-X$ is a positive definite

3. properties of generalized inequlities

A generalized inequality $\preceq_K$ satisfies many properties

  • $\preceq_K$ is preserved under addition（加法保序）
  • $\preceq_K$ is transitive （传递性）
  • $\preceq_K$ is preserved under nonnegative scaling （非负数乘保序）
  • $\preceq_K$ is reflexive: $x\preceq_K x$ (自反性)
  • $\preceq_K$ is antisymmetric: if $x\preceq_K y$ and $y\preceq_K x$, then $x=y$（反对称性）
  • $\preceq_K$ is preserved under limits（极限运算保序）

A strict generalized inequality $\prec_K$ satisfies

  • if $x\prec_K y$ then $x\preceq_K y$
  • if $x\prec_K y$ and $u\prec_K v$ then $x+u\prec_K y+v$
  • if $x\prec_K y$ and $\alpha > 0$ then $\alpha x\prec_K \alpha y$
  • $x\nprec_K y$
  • if $x\prec_K y$ , then for $u$ and $v$ small enough,$x+u\prec_K y+v$ .

4. minimum and minimal elements（最小和极小元）

  • $x \in S$ is the minimum element of $S$ with respect to $\preceq_K$ if $y\in S \Rightarrow x \preceq_K y$
  • $x \in S$ is the minimal element of $S$ with respect to $\preceq_K$ if $y\in S , y\preceq_K x\Rightarrow y=x$

可以对照最小值与极小值的概念理解

Separating and supporting hyperplanes( 分离和支持超平面)

1. Separating hyperplane theorem

Suppose $C$ and $D$ are nonempty disjoint convex sets, i.e., $C \cap D = \emptyset$. Then there exist $a \ne 0$ and $b$ such that $a^T x \le b$f or all $x \in C$ and $a^T x \ge b$ for all $x \in D$. In other words, the affine function $a^T x−b$ is nonpositive on $C$ and nonnegative on $D$. The hyperplane ${x a^T x = b}$ is called a separating hyperplane for the sets $C$ and $D$, or is said to separate the sets $C $and $D$.
  • proof of separating hyperplane theorem
  • strict separation

2. supporting hyperplane theorem

Suppose $C\sube R^n$, and $x_0$ is a point in its boundary $\mathbf{bd} C$, i.e., $x_0 \in \mathbf{bd}C = \mathbf{cl}C \backslash \mathbf{int}C$. If $a \ne 0$ satisfies $a^T x ≤ a^T x_0$ for all $x\in C$, then the hyperplane${ x | a^T x = a^T x_0}$ is called a supporting hyperplane to $C$ at the point $x_0$.

Dual cones and generalized inequalities(对偶锥)

1. Dual cones

$K^* = {y x^T y ≥ 0 {\rm{\ \ for\ all\ }} x \in K}$ is called the dual cone of K, which is a cone.

2.Dual generalized inequalities

  • $x \preceq K y$ if and only if $\lambda ^T x \le \lambda^T y$ for all $λ \ \succeq{K^*} 0$.
  • $x \prec K y$ if and only if $\lambda ^T x < \lambda^T y$ for all $λ \ \succeq{K^*} 0$, $\lambda \ne0$.

课后习题我也做了EE364a的作业，emmm….自己做真的是什么都不会，不知道怎么下手，我是看了看答案理解了再自己写一遍。贴上来没啥意思。就不贴习题了。